Last updated on February 25, 2021
Graphs, a data structure used in the tech industry, displays real-life problems and features of large-scale data. In a previous post, we discussed graph theory terminology and introduced a couple of key applications of graph theory [1]. As a continuation to the previous post, we will explore more representations of graphs as well as other properties and applications.
Challenge Problems
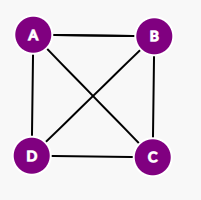
Problem 1: Among a group of 4 people, is it possible for everyone to be friends with exactly 3 of the other people in the group?
Approach: To solve this problem, we can represent a graph where the relation is friendship and each vertex is a person. An edge would indicate that the two vertex connections (people) are friends.
Therefore, we could represent this problem as a graph, such as the figure below, to indicate a possible solution to the problem at hand.
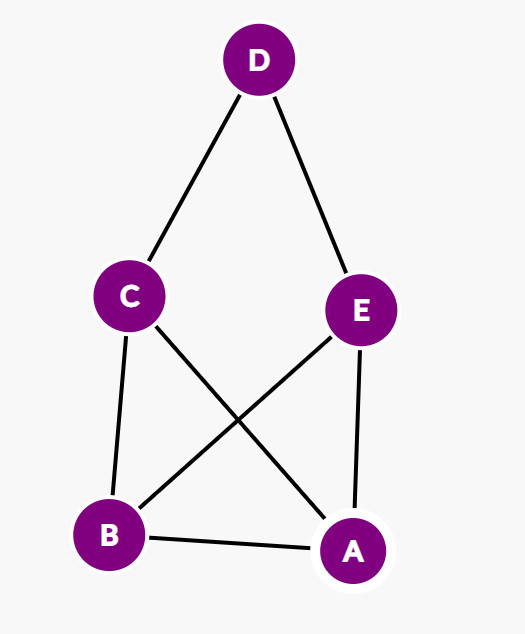
Follow-up Problem 2: Imagine an additional person, Billy, was added to the friend group. Is it still possible for everyone to be friends with exactly 3 of the other people in the group?
Approach: To solve this problem in a brute-force manner, below is an attempted graph that could solve the issue. However, it is no longer possible as proven by the handshaking theorem.
Handshaking Theorem
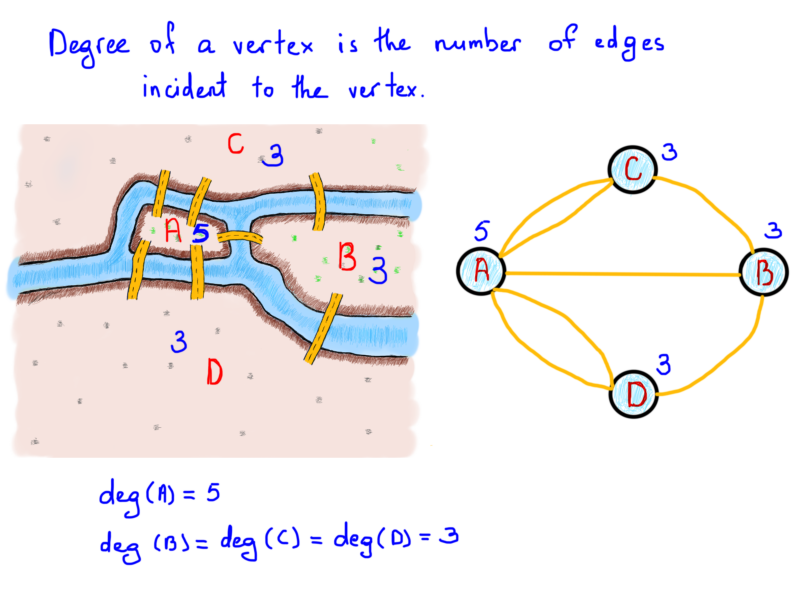
To understand why it is not possible, recall that the degree of a vertex is equal to the number of edges connected to that vertex [2]. In order to create a graph where each vertex has exactly 3 friends would indicate that each vertex has a degree of 3.
Now, in any graph, the sum of the degrees is equal to twice the number of edges presented in a graph. To clarify, view the simple graph below, and notice that nodes A and B both have a degree of 1. The number of edges is 1, and the total sum of degrees is 2.

Because of this ‘handshaking’ property between edges and vertices, we can introduce the handshaking theorem. [3]
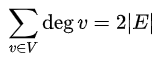
In any graph, the sum of the degrees is only twice the number of edges, which means that the sum of the degrees must be an even number. Revisiting the problem prior, the sum of degrees must be 3 x number of friends, which is 5. 3 x 5 = 15, which is an odd number, and thus violates the handshaking theorem. [3]
As a challenge, is it possible for 10 students, in a group of 11, to hug 2 students, and 1 student to only hug one another student?
Seven Bridges of Konigsburg
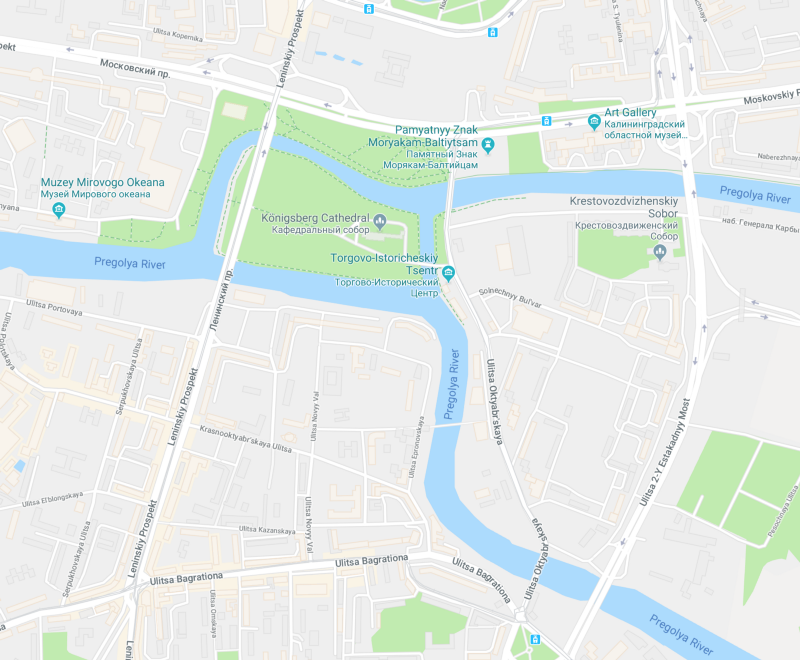
The Seven Bridges of Konigsberg is a notable problem in mathematics, and it laid the foundations for modern day graph theory. This city was set on both sies of the Pregolya River and included two large islands which were connected [4]. The problem was to find a “walk” through the city that would cross each bridge exactly once.
To contextualize, view the transformation from the map to bridges to the graph. The graph denotes an edge as a bridge and each vertex as a landmass.

Key Terms
Walk: More formally, a walk is a key term when it comes to graph theory. A walk in a graph is defined as an alternating sequence between vertices and edges [5].
Trail: A trail is an open/finite walk such that no edge can not be repeated [6].
Path: A path is a trail such that all vertices and edges are distinct [6].
Now after reviewing all of the key terms, the Seven Bridges of Konigsberg is a problem where we are attempting to determine the trail of the path.
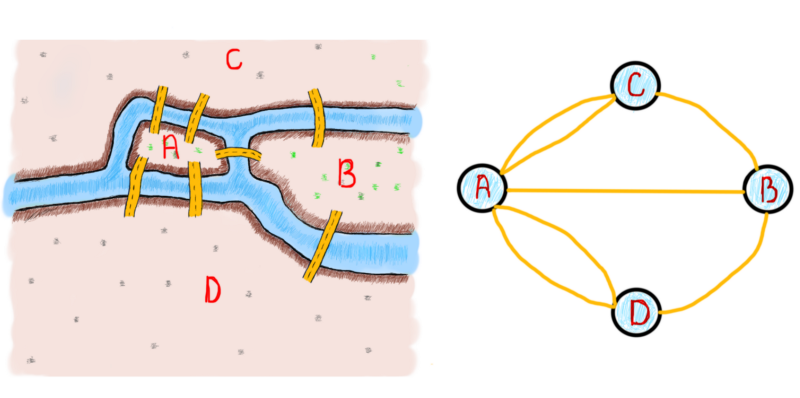
Problem: Can you ‘walk’ throughout this city by crossing each bridge exactly once? [7]
Approach: Similar to earlier, we can attempt this problem by a brute-force approach where we brainstorm all possible solutions and determine whether the condition of crossing each bridge exactly once is upheld.
Now, in Euler’s exploration, he showed that the possibility of a trail through the graph is strictly dependent on the degrees of vertices [7]. Recall that the degree of vertices is the number of edges that that the edge is connected to. Because of Euler’s discovery, this path is known as an Eulerian path in his honor [4].
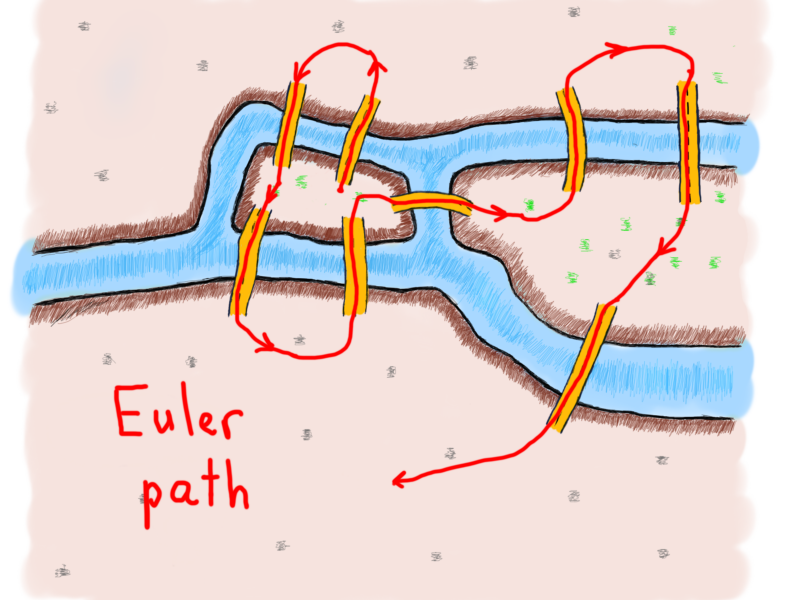
What was Euler’s discoveries exactly and why was it so important? If exactly two vertices are of an odd degree or all vertices are of an even degree then it is said to be a Eulerian graph. Every Euler path of a Euler graph is a path. Otherwise, there is no path [7].
Thinking back on the handshaking theorem, it makes sense that the graph must be even because each entrance to a vertex would need an exit. However, the condition where exactly two vertices can be odd is something to ponder about. Without an additional bridge, no Eulerian path can be formed in the Seven Bridges of Konigsberg.
Isomorphism
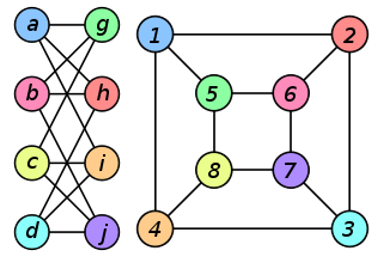
Looking at the two graphs above, it seems at first glance that both graphs are unique (in terms of graph characteristics) but that is not the case. Let’s call the left graph A, and the right graph B. Each vertex of graph A can transforming into a vertex in graph B such that all of the connections will be preserved. To prove two graphs are isomorphic, any two vertices u and v in A are adjacent if and only if f(u) and f(v) are adjacent in B [8].
Now, looking back on the representation of a graph, we can define a graph by either its adjacency matrix or by a list of each edge connection. It is much easier to disprove isomorphism between two graphs rather to prove it.
Ways to disprove:
- The number of vertices in graph A and graph B are not equal [5].
- The number of edges in graph A and B are not equal [9].
- Even though by definition of the handshaking theorem, we know the total sum of degrees is equal to the number of edges. If we are checking for condition 3, then we can assume that the number of edges in graph A and B are equal. However, that does not mean that the number of degrees per edge are equivalent. Each vertex u in graph A must have a vertex v in graph B such that deg(u) = deg(v) [9].
- One graph is cyclic while the other graph is not cyclic [9].
- One graph is connected while the other graph is not [9].
Proving Isomorphism
Now, since we understand ways to disprove two graphs from being isomorphic, let’s attempt to prove the isomorphism between graph A and graph B from earlier.
Firstly, note that each vertex in graph A and graph B has a degree of 3, which means that we may begin to prove isomorphism by assuming vertex a in graph A to be similar to vertex 1 in graph B.
Now, vertex a in graph A is connected to vertex g, vertex h, and vertex i. Similarly, vertex 1 is connected to vertex 2, vertex 5, and vertex 4. Looking at vertex h and vertex i, they share an adjacent vertex, d. Similarly, vertex 2 and vertex 4 share an adjacent vertex, 3. Thus, it can be said that vertex h maps to vertex 2 and vertex i maps to vertex 4.
Continuing to use similar logic to preserve the relations and properties of each vertex, a mapping as such as be made.
f(a) = 1
f(b) = 6
f(c) = 8
f(d) = 3
f(g) = 5
f(h) = 2
f(i) = 4
f(j) = 7
Note that may be several correct mappings, and the answer above is just one possibility.
The motivation behind the idea of isomorphism is that it captures similar graph structures despite visual differences. It may seem easier to analyze graph properties of graph B versus graph A due to the overlapping edge connections.
Bipartite Graphs
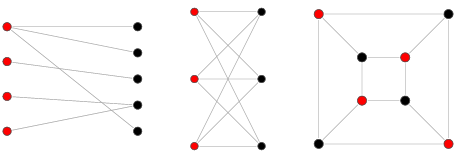
A bigraph, or more formally known as a bipartite graph, is a graph such that the set of vertices can be decomposed into two disjoint sets [10]. Two disjoint sets indicate that no elements in set A are in set B, and vice versa [10]. For example, the set of all irrational numbers and the set of all rational numbers are disjoint sets. Viewing the figure above, it can be apparent in some isomorphic graphs that a graph is a bigraph.
Connecting the concept of graphs with functions, previously taught in math, there is connections between functions and graphs. Before we can view these connections, we must define two key concepts: onto and one-to-one.
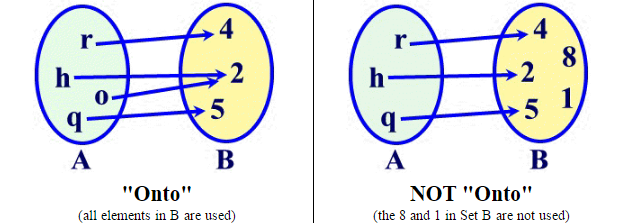
Onto: A function A->B is onto if and only if every element in the co-domain B has a pre-image in A, such that f(a) = b [11]
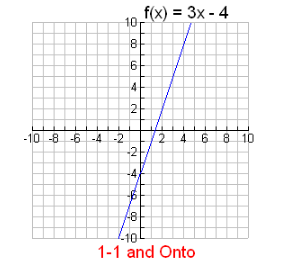
Similarly, a linear function such as 3x-4 is onto, because every element in the range has a valid pre-image in the domain. This makes sense graphically because every y-value has a corresponding x-value.
One-to-one: A function that is one-to-one occurs when every element in the domain has exactly one image in the co-domain [11]. This means that there is a ‘one-to-one’ pairing of each element.
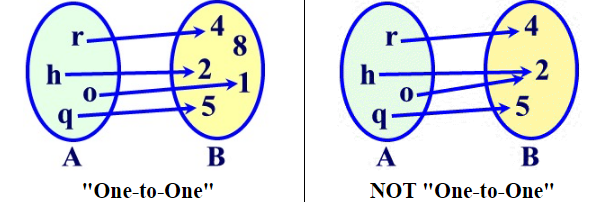
Below is an example of a function that is NOT one-to-one because both an input of 4 and 0 would output a 2. Furthermore, it is not an onto either because there is no possible way to output a negative number, which are in the co-domain of all real numbers.
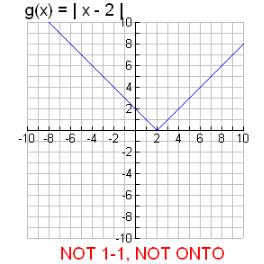
Looking at these definitions, you can see the similarities between bipartite graphs and functions as well as disjoint sets. The applications of bipartite graphs extends into modeling relations particularly for two different type of objects [10]. For example, a graph of football players and clubs where each edge is a relation between a particular player and club would represent a bipartite graph [12]. This is an example of an affiliation network and is used in social network analysis [12]. Bipartite graph properties (onto and one-to-one) extend into defining key attributes of digraphs.
Overall, graphs are among one of the most versatile models of data and relations and are used in an unimaginable amount of applications from path traversals to social networks.
Works Cited
[1] “The Real-Life Applications of Graph Data Structures You Must Know.” https://leapgraph.com/graph-data-structures-applications (accessed Nov. 23, 2020).
[2] Ruohonen, Keijo, Graph Theory. 2013.
[3] “Handshaking Theorem in Graph Theory | Handshaking Lemma | Gate Vidyalay.” https://www.gatevidyalay.com/handshaking-theorem-graph-theory-theorems/ (accessed Feb. 02, 2021).
[4] “Seven Bridges of Königsberg – Wikipedia.” https://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg (accessed Feb. 15, 2021).
[5] “Mathematics | Walks, Trails, Paths, Cycles and Circuits in Graph – GeeksforGeeks.” https://www.geeksforgeeks.org/mathematics-walks-trails-paths-cycles-and-circuits-in-graph/ (accessed Feb. 15, 2021).
[6] “Path (graph theory) – Wikipedia.” https://en.wikipedia.org/wiki/Path_(graph_theory) (accessed Feb. 15, 2021).
[7] “How to think in graphs: An illustrative introduction to Graph Theory and its applications.” https://www.freecodecamp.org/news/i-dont-understand-graph-theory-1c96572a1401/ (accessed Feb. 02, 2021).
[8] “Graph isomorphism – Wikipedia.” https://en.wikipedia.org/wiki/Graph_isomorphism (accessed Feb. 15, 2021).
[9] “big list – Listing methods to prove that two groups are not isomorphic – Mathematics Stack Exchange.” https://math.stackexchange.com/questions/2822469/listing-methods-to-prove-that-two-groups-are-not-isomorphic (accessed Feb. 15, 2021).
[10] “Bipartite Graph — from Wolfram MathWorld.” https://mathworld.wolfram.com/BipartiteGraph.html (accessed Feb. 15, 2021).
[11] “One-to-one and Onto Functions – A Plus Topper.” https://www.aplustopper.com/one-to-one-and-onto-functions/ (accessed Feb. 15, 2021).
[12] “Bipartite graph – Wikipedia.” https://en.wikipedia.org/wiki/Bipartite_graph (accessed Feb. 16, 2021).
Featured Image by Brilliant.org