1 Introduction
Genetic programming (see Sec. 2) is a dynamic evolutionary algorithm that aims to craft programs capable of solving complex problems. At its core, genetic programming employs a mechanism akin to the passage of genetic material from one generation to the next, where programs inherit and adapt their traits (randomly generated functions) over time. This process is analogous to the biological concept of evolution. To simulate the evolutionary process, topics such as diversity (the uniqueness of an individual in a population) are important to the success of genetic programming as it prevents issues such as overfitting, where a program excels at the given test cases but fails to generalize to new inputs. Without a diverse set of genetic programs, each program would function almost exactly like another, preventing progress towards the correct solution. Therefore, test cases are critical to identifying potential flaws in the evolving genetic programs as they help the algorithm generate better solutions to the given problem.
Oracle testing (see Sec. 3) plays a pivotal role in assessing the effectiveness of these genetic programs by comparing their outputs against predetermined expectations. However, as problems grow in complexity, the challenge of developing exhaustive test cases becomes increasingly daunting and costly. This issue highlights the need for alternative testing methodologies that can handle intricate systems more efficiently.
Metamorphic testing (see Sec. 4) emerges as a promising approach in this context, offering a relation-based method to test complex systems. A relation-based method takes advantage of the relationships–or comparisons–between inputs and outputs by verifying whether, for example, the doubling of an input also doubles the output. By defining metamorphic relationships between inputs and their expected outputs, metamorphic testing provides a robust mechanism to identify programmatic bugs. This technique generates its inputs and expects the outputs to follow these defined relationships, allowing for a more automated and scalable testing process. In the realm of genetic programming, where problems can be highly intricate, metamorphic testing shows significant potential in reducing testing costs, improving generalization, and refining the selection process, particularly when combined with selection methods like lexicase selection (see Sec. 2).
In this blog post, we will explore the combination of metamorphic testing and genetic programming (see Sec. 5), demonstrating how this duo can lead to more efficient and effective solutions for complex problems.
2 Genetic Programming
Genetic programming (GP) as an evolutionary algorithm, creates and evolves programs to solve a desired problem. The “genetic” part of GP refers to how each program will pass on their “genes” to the next generation. To determine which genes are passed from one individual (a program amongst the entire population) to the next, we must establish a selection algorithm. While there are many different selection algorithms (each with their own benefits), we will focus on lexicase selection as the paper that inspired this blog post uses it.
Before we evaluate how individuals are selected, an important concept in GP is the diversity of a population. Diversity is often determined by the similarity of an individuals’ answer in comparison to the rest of the population. GP algorithms prefer to have a diverse population because there are times where programs will form a large bubble when the correct answer is nearby. In other words, the algorithm promotes one answer and disregards other solutions, even if there are better answers.
Next, for the selection process to find the best individual to pass traits from, we must first evaluate the fitness of an individual. Fitness (a program’s ability to solve the given problem) can be measured in a variety of ways; most of which prioritize the diversity of a population to prevent any overfitting issues (inability to improve beyond the scope of the training data).
For this example, fitness will be calculated as an error value, where a large number is a bad fitness value and a 0 indicates a perfect fitness value. Typically, this would be done amongst hundreds of individuals per population, and the process for selecting new individuals can vary as genetic programs try to maintain diversity.
Back to lexicase selection, after determining the error values of each program for each test case (see Table 1), we can begin to select the best individuals. To further understand this method, lexicase selection continuously evaluates random test cases for all programs until one is left–the selected individual is called a parent which passes parts of its genetic structure to its child.
| Test 1 | Test 2 | Test 3 | |
|---|---|---|---|
| A | 1 | 3 | 12 |
| B | 2 | 1 | 4 |
| C | 0 | 10 | 4 |
Table 1: A representation for lexicase selection with programs A, B, and C with their corresponding error values.
As an example, we can see that Table 1 has three different program individuals A, B, and C. Lexicase selection will randomly choose a test case to check. Let’s say it chooses Test 3. It will find the smallest error (in this case B and C with error values of 4 and 4) and eliminate the others.
If there are still programs left, we repeat the process with a new test case. In that case, because we have two individuals left (B and C), if Test 1 is selected, only program C will remain as it has the lowest error value of 0. Thus, program C is selected regardless of the remaining test cases.
However, not all test cases provide a wide enough net to capture all general errors. Because test cases are often not exhaustive of all possible inputs and outputs, sometimes bugs slip through without notice. Test cases are especially important for GP algorithms, as without an appropriate amount of data to mutate individuals, at best we would get a random blob that outputs nonsense (or, we get extremely lucky). So, to create general enough test cases such that we can solve for any input, we need to create unique, yet general, test cases.
3 Oracle Testing
An oracle checks a program’s efficacy by comparing an experimental output with the expected one. Accompanied with test cases, oracles give a pass or a fail depending on how the program reacts to each test.
There are different versions of oracle testing ranging from human to program testers. Most, if not all oracle testing, has predetermined outputs that the program tests for and is designed by a human. After creating the outputs, we compare them with the human-created outputs. If they do not match, the program fails and we need to resolve the issue.
For simpler systems that require limited testing, oracles are very effective. Because oracles compare against an expected output, researchers can continually test against that output and tweak their program such that it fits the desired output for each test case. Additionally, since the program is simple, the test cases are likely to be exhaustive such that they cover any abnormality the given problem may have.
However, one of the biggest issues with oracle testing is that with increasing complexity, it becomes more expensive to cover all possible test cases [5].
As a quick definition, expensiveness is primarily measured as the time and effort it takes to come up with test cases to cover lots of ground.
Since the problem is complex and a human often develops the test cases, it becomes difficult for a researcher to cover the bases needed to ensure the program is correct.
Without proper testing, the test results may lead a developer to believe their program works for all cases, when in fact there could exist at least one case where it fails.
4 Metamorphic Testing
Metamorphic testing is a relation-based approach for testing complex systems. For example, if a given input is manipulated or modified in a particular way, then the output should also represent the same change. The relationship is some mathematical property between the input and the output. If this relationship is violated in some way, then there is a bug in the program. This relationship is known as a metamorphic relationship [1, 2, 3]. For further understanding, please consider the following example.
The vector u = <3, 4> is our input and our theoretical program calculates the norm of the vector u. Therefore,
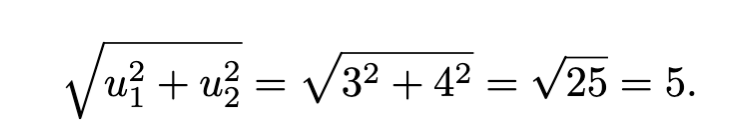
If we morph the input to be twice the size, or 2u, then the vector would be 2u = u’ = <6, 8>. Then it follows that,
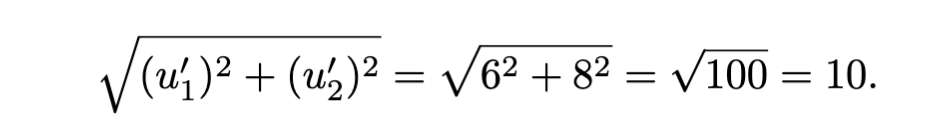
The metamorphic relationship between u and u’ is multiplying u by 2, or 2u = u’. We can see in the answer that we have such a relationship, 5 = (2)5.
That’s about all there is to it. Metamorphic testing generates its own inputs, and based on those inputs will expect the outputs to share the same metamorphic relationships such as the one between u and u’.
Research about metamorphic testing is still ongoing. However, the benefits of metamorphic testing for programmers and researchers are still relevant as it removes the oracle problem.
5 Metamorphic Testing in GP
Finally, the culmination of this blog post: Metamorphic Testing in Genetic Programming (MTGP). From here, we will examine some of the data from the paper, MTGP: Combining Metamorphic Testing and Genetic Programming by Sobania et al. which utilizes a grammar-guided genetic programming approach with lexicase selection.
Grammar-guided GP (GGGP) is a GP approach that uses context-free grammar (CFG) to create programs recursively. As a quick example, let’s assume the following rules for a CFG [6, 7]:
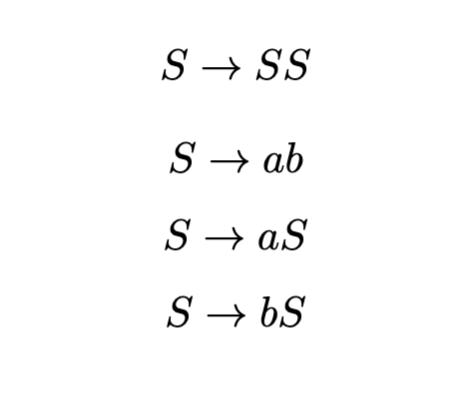
This means that the letter ‘S’ (singular) maps to four outputs [SS, ab, aS, and bS].
To produce an output string such as, “aaabbabbab,” the following tree would suffice [8]:
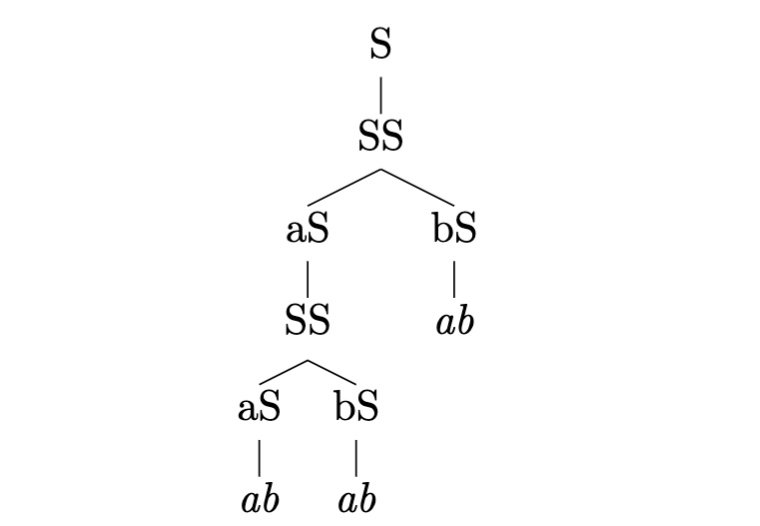
The paper proposes MTGP as a better alternative to oracle testing when it comes to solving complex problems. There are three main benefits: low costs for complex problems, better generalization to unseen problems, and a more refined selection process when using lexicase selection.
The low costs circle back to the oracle problem. When creating test cases for programs, people hand-create the test cases which can take an unnecessarily long time to do. Especially for programs that are difficult to create test cases for, many issues may go unresolved until much later. Or, researchers may believe they found a solution to a particular problem when in fact they had missed a crucial step in the process.
However, with MTGP, only a few cases would need to be hand-written. In fact, the paper found that test cases with improved generalization rates included a mix of hand-written test cases alongside metamorphic test cases. The generalization rate (GR) refers to the performance of a program in terms of unseen test cases.
GRs in the paper were calculated by dividing the successful test rate by the successful training rate and multiplying that number by 100. To put this into perspective, the GR Sobania et al. used was
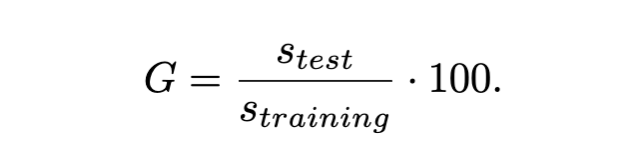
From here, they noticed that out of the nine test cases, MTGP had a higher GR in seven of them. The researchers then tried to see what would happen if they increased the number of metamorphic tests, and in all cases MTGP outperformed standard GP.
This data means that the programs are general enough such that they do not create solutions just to solve the training set, but rather can solve cases that are outside of its original scope. For example, if you have a program that can solve a Rubik’s cube in thirty different starting positions, and it can solve the cube in more than 100 starting positions, then you can say it has a high generalization rate. In fact, it may be the case that it can solve a cube in any position.
The third benefit to MTGP was the improvement it provided to lexicase selection. For an example of lexicase selection, we will be using Table 2. For MTGP, this selection method works quite well. Since lexicase selection continuously evaluates random test cases for all programs until one program is left, with metamorphic testing, we can check to see if the metamorphic relation holds for each test case.
| Test 1 | Test 2 | Test 3 | M-Test | |
|---|---|---|---|---|
| A | 1 | 3 | 12 | True |
| B | 2 | 1 | 4 | True |
| C | 0 | 10 | 4 | False |
With the inclusion of metamorphic testing, programs will not only have to check if their initial outputs have a low error value compared to the expected value, but also if their algorithm holds for a given metamorphic relation. Let’s imagine that we are still choosing between programs B and C under Test Case 1 (continuing from Sec. 2’s example). While program C has an error value of 0, it’s metamorphic relationship is false, which indicates that these error values will not be consistent with different inputs.
On the other hand, program B’s metamorphic relation holds. Therefore, program B is selected. In other words, metamorphic testing adds another layer to lexicase selection and allows individuals whose algorithms are consistent to pass on their traits to future generations.
6 Conclusion
In conclusion, metamorphic testing has emerged as a powerful and innovative approach in the field of genetic programming. While genetic programming is not yet ready for wide-scale usage, the combination of metamorphic testing and genetic programming allows us to take another step in the right direction. By leveraging the principles of metamorphic relations, this technique not only enhances the generalization of genetic programming algorithms but also aids in reducing the costs of oracle testing and improving lexicase selection. Its potential to increase the efficacy of the evolutionary process underscores its significance in shaping the future of genetic programming research and applications.
References
[1] MTGP: Combining Metamorphic Testing and Genetic Programming, Sobania et al.
[2] A Field Guide to Genetic Programming, Poli, Ricardo et. al.
[3] Metamorphic Testing, Hillel Wayne
[4] The Oracle Problem in Software Testing: A Survey, Barr, Earl T et al
[5] What is Context Free Grammar?
[6] A Grammar Design Pattern for Arbitrary Program Synthesis Problems in Genetic Programming, Forstenlechner, Stefan


